交流電路中的有源電阻和電感

考慮僅包含電感電阻的交流電路（參見文章 «交流電路中的電感器»)，我們假設該電路的有源電阻為零。

事實上，無論是線圈本身的導線還是連接導線都有一個很小但有源的電阻，所以電路不可避免地要消耗電流源的能量。

因此，在確定外電路的總電阻時，需要加上它的無功電阻和有源電阻。但是不可能將這兩種性質不同的電阻相加。

在這種情況下，電路對交流電的阻抗是通過幾何加法求得的。

構造一個直角三角形（見圖1），其中一側為感性電阻值，另一側為有源電阻值。所需的電路阻抗由三角形的第三條邊決定。

圖 1. 確定包含電感和有源電阻的電路的阻抗

電路阻抗用拉丁字母 Z 表示，單位為歐姆。從構造中可以看出，總電阻總是大於單獨取的電感和有源電阻。

總電路電阻的代數表達式為：

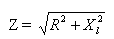
其中Z——總電阻，R——有源電阻，XL——電路的感性電阻。

因此，由有源電阻和感性電阻組成的電路對交流電的總電阻等於該電路的有源電阻和感性電阻的平方和的平方根。

歐姆定律 因為這樣的電路由公式 I = U / Z 表示，其中 Z 是電路的總電阻。

現在讓我們分析一下，如果電路除了電流和電感之間的相移之外，還有一個比較大的有源電阻，電壓會是多少。在實踐中，這樣的電路可以是例如包含用細線繞製的鐵芯電感器（高頻扼流圈）的電路。

在這種情況下，電流和電壓之間的相移將不再是四分之一周期（就像在只有電感電阻的電路中那樣），而是更小；電阻越大，產生的相移越小。

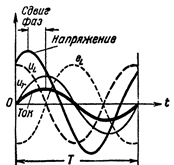
圖 2. 包含 R 和 L 的電路中的電流和電壓。

現在她自己 自感電動勢 與電流源電壓不反相，因為它相對於電壓偏移不是半個週期，而是更少。另外，電流源在線圈兩端產生的電壓不等於自感電動勢，而是比自感電動勢大了線圈導線有源電阻的壓降量。換句話說，線圈中的電壓無論如何都由兩個部分組成：

• tiL- 電壓的無功分量，它平衡了自感應 EMF 的影響，

• tiR- 將克服電路有源電阻的電壓的有源分量。

如果我們在線圈上串聯一個大的有源電阻，相移會減小很多，電流正弦波幾乎趕上電壓正弦波，它們之間的相位差幾乎看不出來。在這種情況下，項的振幅，並且將大於項的振幅。

同樣，如果以某種方式降低發生器的頻率，則可以降低相移，甚至可以將其完全降低為零。頻率的降低將導致自感電動勢的降低，因此導致電路中電流和電壓之間的相移減小。

包含電感器的交流電路的功率

含有線圈的交流電路不消耗電流源的能量，電路中發電機與電路之間存在能量交換過程。

現在讓我們分析一下這種方案消耗的功率會怎樣。

交流電路中消耗的功率等於電流和電壓的乘積，但由於電流和電壓是可變量，那麼功率也將是可變的。在這種情況下，如果我們將電流值乘以給定時刻對應的電壓值，就可以確定每個時刻的功率值。

要得到功率圖，我們需要將定義不同時間的電流和電壓的直線段的值相乘。這種結構如圖 1 所示。 3、一個。虛線波形 p 向我們展示了功率如何在僅包含電感電阻的交流電路中變化。

在構造這條曲線時使用了以下代數乘法規則：當一個正值乘以一個負值時，得到一個負值，當兩個負值或兩個正值相乘時，得到一個正值。

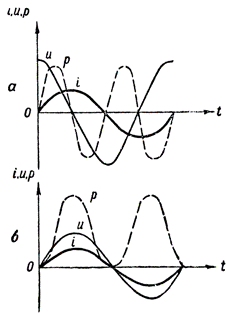
圖 3. 功率圖：a — 在包含電感電阻的電路中，b — 同樣，有源電阻

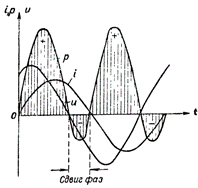
圖 4. 包含 R 和 L 的電路的功率圖。

這種情況下的功率曲線位於時間軸上方。這意味著發電機和電路之間沒有能量交換，因此發電機提供給電路的功率完全被電路消耗掉了。

在圖。圖 4 顯示了包含電感和有源電阻的電路的功率圖。在這種情況下，也會發生從電路到電流源的能量反向傳輸，但程度遠低於具有單個電感電阻的電路。

查看以上功率圖後，我們得出結論，只有電路中電流和電壓之間的相移會產生“負”功率。在這種情況下，電路中電流和電壓之間的相移越大，電路消耗的功率就越小，反之，相移越小，電路消耗的功率就越大。

另請閱讀： 什麼是電壓諧振