單相變壓器的工作原理和裝置
單相空載變壓器
電氣工程中的變壓器被稱為這樣的電氣設備,其中來自一個固定線圈的交流電能被傳輸到另一個未與第一個線圈電連接的固定線圈。
將能量從一個線圈傳輸到另一個的鏈接是磁通量,它與兩個線圈互鎖,並且在大小和方向上不斷變化。
米。 1.
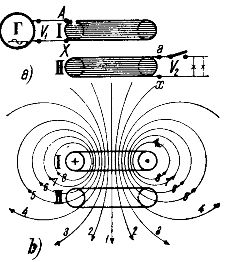
在圖。圖 1a 顯示了由兩個繞組 / 和 / / 組成的最簡單的變壓器,一個在另一個上面同軸排列。到卷/交付 交流電 來自交流發電機 D。該繞組稱為初級繞組或初級繞組。繞組 // 稱為次級繞組或次級繞組,電路通過電能接收器連接。

變壓器的工作原理
變壓器的動作如下。當電流在初級繞組中流動時/它被創建 磁場,其力線不僅滲透到產生它們的繞組中,而且還部分滲透到次級繞組中 //。初級繞組產生的力線分佈的近似圖如圖 1 所示。 1b.
從圖中可以看出,所有的力線都是圍繞線圈/的導體閉合的,但在圖在圖 1b 中,電線 1、2、3、4 也閉合在線圈 // 的電線周圍。因此線圈//通過磁力線磁耦合到線圈/。
線圈/和//同軸佈置的磁耦合程度取決於它們之間的距離:線圈彼此距離越遠,它們之間的磁耦合越小,因為作用在線圈上的力線越少線圈/粘在線圈上//。
由於線圈 / 通過,正如我們假設的那樣, 單相交流電,也就是電流隨著時間的推移按照某種規律變化,比如按照正弦規律,那麼它產生的磁場也會按照同樣的規律隨時間變化。
例如,當線圈中的電流/通過最大值時,則其產生的磁通量也通過最大值;當線圈中的電流/通過零時,方向改變,則磁通量也通過零,方向也改變。
由於改變線圈 / 中的電流,線圈 / 和 // 都被磁通量穿透,不斷改變其值和方向。根據電磁感應的基本定律,穿過線圈的磁通量每發生變化,線圈中就會感應出交流電 電動勢……在我們的例子中,自感電動勢是在線圈/中感應出來的,而互感電動勢是在線圈//中感應出來的。
如果線圈的末端 // 連接到電能接收器電路(見圖 1a),則該電路中將出現電流;因此接收器將接收電力。同時,能量將被引導至繞組/從發電機,幾乎等於繞組//提供給電路的能量。這樣,來自一個線圈的電能將傳輸到第二個線圈的電路,第二個線圈與第一個線圈在電流(金屬)上完全無關,在這種情況下,能量傳輸的方式只是交變磁通量。
如圖所示1a,變壓器非常不完善,因為初級繞組/和次級繞組//之間幾乎沒有磁耦合。
一般而言,兩個線圈的磁耦合是通過耦合到兩個線圈的磁通量與一個線圈產生的磁通量之比來估計的。
如圖。從圖1b可以看出,只有線圈/的部分磁力線在線圈//周圍閉合。電源線的另一部分(在圖 1b 中——線 6、7、8)僅在線圈 / 周圍閉合。這些電源線根本不參與從第一個線圈到第二個線圈的電能傳輸,它們形成所謂的雜散場。
為了增加初級和次級繞組之間的磁耦合,同時降低磁通通過的磁阻,技術變壓器的繞組放置在完全封閉的鐵芯上。
圖 1 示意性地顯示了變壓器實施的第一個示例。 2 所謂棒式單相變壓器。其初級、次級線圈c1、c2裝在鐵棒a—a上,兩端接有鐵板b—b,稱為磁軛。這樣,兩個桿a、a和兩個磁軛b、b組成一個閉合的鐵環,其中通過被初級和次級繞組阻擋的磁通量。這個鐵環就叫做變壓器的鐵芯。
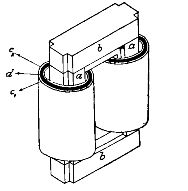 米。 2.
米。 2.
變壓器的第二個實施例示意性地顯示在圖1中。 3 所謂的鎧裝型單相變壓器。在這個變壓器中,初級和次級繞組 c,每個都由一排扁平繞組組成,放置在由兩個鐵環 a 和 b 的兩根桿形成的鐵芯上。圍繞繞組的環 a 和 b 幾乎完全覆蓋有鎧裝,因此所描述的變壓器稱為鎧裝變壓器。通過線圈 c 內部的磁通量被分成相等的兩部分,每一部分都被封閉在自己的鐵環中。
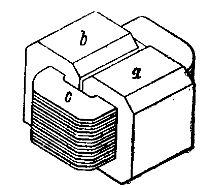
米。 3個
在變壓器中使用閉合鐵磁路可顯著降低洩漏電流。在這種變壓器中,連接到初級和次級繞組的磁通幾乎彼此相等。如果我們假設初級和次級繞組被相同的磁通量穿透,我們可以根據繞組電動勢的瞬時值的總感應衝擊寫出表達式:
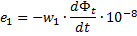
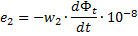
在這些表達式中,w1和w2——初級和次級繞組的匝數,dFt是每個時間元dt的磁通量在穿透繞組中的變化幅度,因此存在磁通量變化率.從最後的表達式,可以得到以下關係:
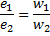
IE。在初級和次級繞組/和//中表示的瞬時電動勢以與線圈匝數相同的方式相互關聯。最後的結論不僅對電動勢的瞬時值有效,而且對它們的最大有效值也有效。
在初級繞組中感應出的電動勢,作為自感電動勢,幾乎完全平衡施加在同一繞組上的電壓...如果用E1和U1你表示電動勢的有效值 \u200b\u200b初級繞組和施加在它上面的電壓,那麼你可以寫:
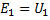
在所考慮的情況下,次級繞組中感應的電動勢等於該繞組兩端的電壓。
如果像上一個一樣,通過E2和U2表示次級繞組的電動勢有效值和兩端電壓,那麼你可以寫:
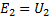
因此,通過在變壓器的一個繞組上施加一些電壓,您可以在另一個線圈的末端獲得任何電壓,您只需要在這些線圈的匝數之間取一個合適的比率即可。這就是變壓器的主要特性。
初級繞組匝數與次級繞組匝數之比稱為 變壓器變壓比... 我們將表示變換係數 kT。
因此,可以這樣寫:
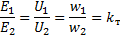
變比小於1的變壓器稱為升壓變壓器,因為次級繞組的電壓,或所謂的次級電壓,大於初級繞組的電壓,或所謂的初級電壓.變比大於1的變壓器稱為降壓變壓器,因為它的次級電壓小於初級。

單相變壓器帶載運行
在變壓器空轉期間,磁通量由初級繞組電流或初級繞組的磁動勢產生。由於變壓器的磁路由鐵製成,因此磁阻小,一般假定初級繞組的匝數較大,變壓器的空載電流較小,為5-正常值的 10%。
如果把次級線圈接上某個電阻,那麼隨著次級線圈中電流的出現,這個線圈的磁動勢也會出現。
根據楞次定律,次級線圈的磁動勢與初級線圈的磁動勢相反
看起來這種情況下的磁通量應該會減少,但如果在初級繞組上施加恆定電壓,那麼磁通量幾乎不會減少。
實際上,變壓器帶載時在初級繞組中感應的電動勢幾乎等於外加電壓。該電動勢與磁通量成正比。因此,如果初級電壓大小恆定,則負載下的電動勢應與變壓器空載運行期間的電動勢幾乎相同。這種情況導致磁通量在任何負載下幾乎完全恆定。
 因此,在初級電壓恆定值下,變壓器的磁通量幾乎不隨負載的變化而變化,可以假設與空載運行時的磁通量相等。
因此,在初級電壓恆定值下,變壓器的磁通量幾乎不隨負載的變化而變化,可以假設與空載運行時的磁通量相等。
變壓器的磁通量之所以能夠在負載下保持其值,只是因為隨著次級繞組中出現電流,初級繞組中的電流也增加,以至於初級和次級的磁動勢或安匝數之間存在差異繞組在空轉期間保持幾乎等於磁動勢或安匝數……因此,次級繞組中退磁磁動勢或安匝數的出現伴隨著初級繞組磁動勢的自動增加。
如上所述,由於產生變壓器磁通需要較小的磁動勢,因此可以說次級磁動勢的增加伴隨著初級磁動勢的增加,其大小幾乎相同。
因此,可以這樣寫:
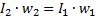
從這個等式可以得到變壓器的第二個主要特性,即比率:
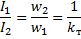
其中 kt 是轉換因子。
因此,變壓器初級和次級繞組的電流之比等於1除以變壓比。
所以, 變壓器的主要特性 有關係
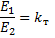
和
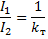
如果我們將關係的左側相乘,右側相乘,我們得到
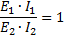
和
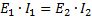
最後一個等式給出了變壓器的第三個特性,可以用這樣的話來表示:變壓器次級繞組傳遞的功率(以伏安表示)幾乎等於傳遞給初級繞組的功率(以伏安表示) .
如果我們忽略繞組銅和變壓器鐵芯中的能量損失,那麼我們可以說從電源提供給變壓器初級繞組的所有功率都轉移到了它的次級繞組,並且發射機是磁通量。
