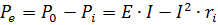電路中的功率平衡

根據 焦耳-楞次定律 直流電在電阻中所做的功，

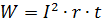
如果另一個將電磁能轉換為機械能或化學能或其他形式的能量（電動機、充電電池等）的轉換器代替電阻器包含在所考慮的支路中，則電流在時間 t 內所做的功可以計算為如果轉換器電壓已知的情況。

在這種情況下，Joule-Lenz 公式採用不同的形式：

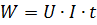
在直流電下，提供給電阻為 r 的電路部分的功率由以下表達式給出：

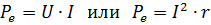
其中 I、U 和 r 保留與 Joule-Lenz 公式中相同的含義。

整個外電路消耗的功率和發電機提供的功率是一樣的。發電機產生的功率總是大於發電機提供給外部電路的功率，因為一部分功率用於彌補發電機本身內部的損耗。

單個閉環的功率平衡表達式包含一個具有電動勢 E 和內阻 ri 的發電機和一個電阻為 r 的電阻器，可以從基爾霍夫方程中獲得。

對於這個電路

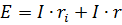
如果這個等式的兩邊都乘以電路中的電流，那麼得到的等式將代表該電路中的功率平衡

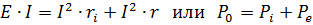
發電機產生的功率等於發電機內部損失並提供給外電路的功率之和。 P0=EI為發電機發出的功率，Pe=UI=I2r為發電機給外電路的功率，Pi—I2ri為發電機內部損失的功率。

當雙端I流過的電流和雙端U的電壓選擇相同的正方向時，兩端消耗的功率，即產品的用戶界面，必須為正。如果同時發現產品的用戶界面為負，這將意味著具有兩個端子的設備不消耗電磁能，相反，它是電磁能的發生器，並將該能量提供給 電路.

如果在電路中有多個具有兩個端子的設備向電路發射電磁能，則其他設備會吸收該能量。在直流電路中，不會發生電磁能量的積累。因此，無源兩端網絡消耗的功率與發電機內部損失的功率之和必須等於所有發電機產生的功率的代數和，即在一個電路中工作的所有發電機的乘積 EkIk 的總和：

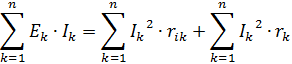
其中 n — 鏈中的分支數。

對於包含一個發電機的簡單電路獲得的平衡方程可以通過將外部電路中消耗的功率表示為發電機表示的功率和發電機內部損失的功率來重寫：