載流線圈的磁場

如果靜電場存在於靜止電荷周圍的空間，那麼在運動電荷周圍的空間（以及麥克斯韋最初提出的時變電場周圍）也存在 磁場……這很容易通過實驗觀察到。

由於磁場，電流相互作用，永磁體和電流與磁鐵相互作用。與電相互作用相比，磁相互作用要強得多。 André-Marie Ampère 在適當的時候研究了這種相互作用。

在物理學中，磁場特性是 磁感應 B越大，磁場越強。磁感應強度 B 是一個矢量，它的方向與磁場中某點放置的常規磁箭頭的北極所受力的方向一致——磁場會使磁箭頭指向矢量方向B，即磁場方向。

磁感應線上任一點的向量 B 都切向指向它。即感應強度B表徵磁場對電流的力作用。電場的力 E 也起著類似的作用，它表徵了電場對電荷的強烈作用。

最簡單的鐵屑實驗可以讓你清楚地演示磁場對磁化物體的作用現象，因為在恆定磁場中，鐵磁體的小塊（這樣的碎片是鐵屑）沿磁場被磁化，磁性箭頭，就像指南針的小箭頭。

如果你拿一根垂直的銅線穿過水平放置的紙（或有機玻璃或膠合板）上的孔，然後將金屬屑倒在紙上，稍微搖晃一下，然後讓直流電通過電線，很容易看出鐵屑如何以渦流的形式圍繞電線繞圈，在垂直於其中電流的平面內。

這些鋸屑圈將只是載流導體磁場的磁感應線 B 的常規表示。本實驗中的圓心將恰好位於載流導線軸線的中心。

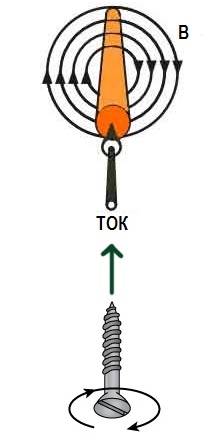
載流導線中磁感應矢量的方向很容易確定 通過手鑽規則 或根據右手螺旋定則：隨著螺旋軸沿導線中電流方向的平移運動，螺旋或萬向節手柄的旋轉方向（旋入或旋出）將指示導線的方向電流周圍的磁場。

為什麼應用萬向節規則？因為兩個麥克斯韋方程中使用的轉子的功（在場論中用衰減表示）可以正式地寫成向量積（使用算符 nabla），最重要的是因為向量場的轉子可以比作 ( 是一個類比）到理想流體的旋轉角速度（如麥克斯韋自己想像的那樣），其流速場表示給定的矢量場，可以通過為角速度描述的這些規則公式用於轉子。

因此，如果您將拇指朝矢量場渦流的方向轉動，它就會朝該場轉子矢量的方向旋轉。

如您所見，與空間中開放的靜電場強度線不同，電流周圍的磁感應線是閉合的。如果電場強度線 E 以正電荷開始並以負電荷結束，那麼磁感應線 B 就簡單地閉合在產生它們的電流周圍。

現在讓我們把實驗複雜化。考慮用電流彎曲而不是直的電流。假設我們可以方便地將這樣一個環路垂直於繪圖平面放置，電流在左側流向我們，在右側流向我們。如果現在將一個帶有磁針的羅盤放在電流環路內，那麼磁針將指示磁感應線的方向——它們將沿著環路的軸方向。

為什麼？由於線圈平面的相對側類似於磁針的兩極。B 線離開的地方是北磁極，在那裡它們進入南極。如果您首先考慮載流導線及其磁場，然後將導線簡單地繞成一個環，這就很容易理解了。

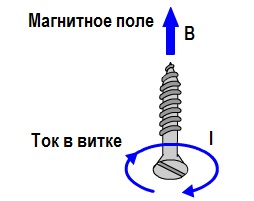
為了確定通電迴路的磁感應方向，他們還使用萬向節定則或右手螺旋定則。將萬向架的尖端放在環的中心並順時針旋轉。萬向節的平移運動將與環中心的磁感應矢量 B 的方向一致。

顯然，電流磁場的方向與導線中電流的方向有關，無論是直導線還是線圈。

一般認為，載流線圈或線圈中磁感應線 B 出射（矢量 B 方向向外）的一側為北磁極，磁感應線進入（矢量 B 方向向內）的一側為磁北極。南磁極。

如果通電的許多匝組成一個長線圈——螺線管（線圈的長度是其直徑的許多倍），則其內部的磁場是均勻的，即磁感應線B相互平行且具有沿線圈的整個長度具有相同的密度。順便提及，永磁體的磁場在外部類似於通電線圈的磁場。

對於電流為 I、長度為 l、匝數為 N 的線圈，真空中的磁感應強度在數值上等於：

因此，帶電流的線圈內部的磁場是均勻的，並且從南極指向北極（在線圈內部！）。線圈內的磁感應強度與載流線圈每單位長度的安匝數成模數正比。