電磁振動——無阻尼和強迫振動

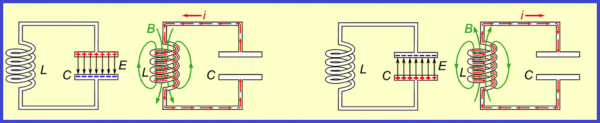
由電感器和電容器組成的電路中的電磁振動是由於電能與磁能的周期性轉換而發生的，反之亦然。在這種情況下，電容器極板上的電荷和通過線圈的電流大小會周期性變化。

電磁振動是自由的和強制的。通常，自由振盪由於非零環路電阻而被阻尼，而強制振盪通常是自振盪。

獲得 在振動電路中 自由振盪，我們首先需要使這個系統失去平衡：用初始電荷 q0 通知電容器或以某種方式啟動電流脈衝 I0 通過線圈。

這將作為一種脈衝，電路中將發生自由電磁振盪 - 電容器通過感應線圈的交替充電和放電過程將開始，相應地，線圈磁場的可變上升和下降

由外部交變電動勢在電路中維持的振盪稱為強迫振盪。因此，正如您已經了解的那樣，可以觀察到自由電磁振蕩的最簡單振盪系統的示例是由電容 C 的電容器和電感 L 的線圈組成的振盪電路。

在真實的振盪電路中，電容器的充電過程會周期性重複，但振盪很快就會消失，因為能量主要消耗在線圈導線的有源電阻 R 上。

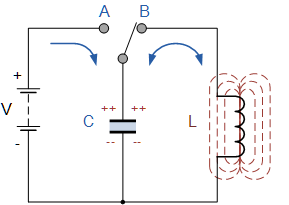
考慮一個具有理想振盪電路的電路。讓我們首先用電池給電容器充電——我們將給它初始電荷 q0，也就是說，我們將用能量填充電容器。這將是電容器 We 的最大能量。

下一步是斷開電容器與電池的連接，並將其與電感並聯。此時，電容器將開始放電，線圈電路中將出現增加的電流。電容器放電的時間越長，它逐漸進入線圈的電荷就越多，線圈中的電流就越大，因此線圈以磁場的形式儲存能量。

這個過程不是瞬間發生的，而是逐漸發生的，因為線圈有電感，也就是說會出現自感現象，就是線圈無論如何都會抵抗電流的增加。在某一時刻，線圈的磁場能量達到最大可能值 Wm（取決於最初轉移到電容器的電荷量以及電路的電阻）。

另外，由於自感現象，通過線圈的電流保持方向相同，但幅度減小，電荷最終再次積聚在電容器中。以這種方式，電容器被再充電。它的極板現在具有與實驗開始時相反的電荷符號，當時我們將電容器連接到電池。

電容器能量已達到此電路的最大可能值。電路中的電流已停止。現在這個過程開始朝相反的方向發展，而且會一次又一次地繼續，也就是說，會有自由的電磁振盪。

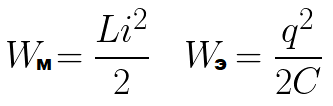
如果電路的有源電阻 R 等於零，則電容器板兩端的電壓和通過線圈的電流將根據諧波定律 - 餘弦或正弦無限變化。這稱為諧波振動。電容器板上的電荷也會根據諧波定律發生變化。

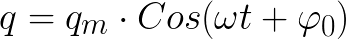
理想循環中沒有損失。如果是，那麼電路中的自由振盪週期將僅取決於電容器的電容 C 和線圈的電感 L 的值。可以使用 Thomson 公式找到這個週期（對於 R = 0 的理想循環）：

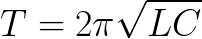
使用以下公式可以找到理想無損電路的相應頻率和循環頻率：

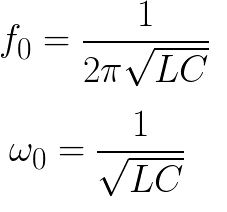
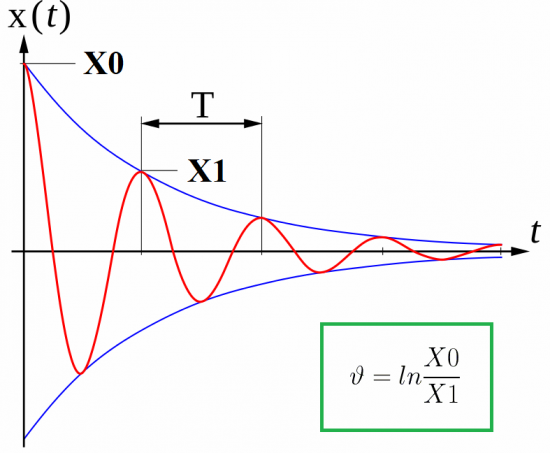
但理想的電路並不存在，並且電磁振盪會因電線發熱造成的損耗而衰減。根據電路電阻 R 的值，每個後續的最大電容器電壓將低於前一個。

針對這種現象，物理學中引入了振蕩的對數衰減量或阻尼衰減量這樣的參數。它被發現為振蕩的兩個連續最大值（具有相同符號）之比的自然對數：

對數振盪衰減通過以下關係與理想振盪週期相關，其中可以引入一個附加參數，即所謂阻尼因子：

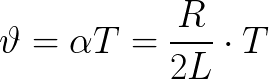
阻尼影響自由振動的頻率。因此，計算實際振盪電路中自由阻尼振盪頻率的公式與理想電路（考慮阻尼係數）的公式不同：

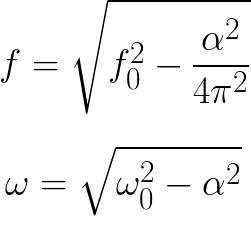
使電路產生振盪 取消靜音，需要每半個週期補充和補償這些損失。這是在連續振盪發電機中實現的，其中外部 EMF 源用其能量補償熱損失。這種具有外部 EMF 源的振盪系統稱為自振盪。