異步電機運行

感應電機的運行以圖形方式表示速度 n2、效率 η、有用轉矩（軸轉矩）M2、功率因數 cos φ 和定子電流 I1 在 U1 = const f1 = const 時對有用功率 P2 的依賴性。

速度特性n2=f(P2)。感應電動機的轉子速度 n2 = n1 (1 — s)。

載玻片 s = Pe2 / Rem，即感應電機的滑差及其速度由轉子中的電損耗與電磁功率之比決定。忽略空轉時轉子的電損耗，我們可以取 Pe2 = 0，因此 s ≈ 0 和 n20 ≈ n1。

隨著軸負載的增加 異步引擎 比率 s = Pe2 / Pem 增加，在額定負載下達到 0.01 - 0.08 的值。因此，依賴性n2＝f(P2)是稍微向橫坐標軸傾斜的曲線。然而，隨著電機轉子有源電阻r2'的增大，該曲線的斜率增大。在這種情況下，隨著負載P2的波動，感應電動機n2的頻率變化增加。這是因為當 r2 ' 增加時，轉子中的電損耗增加。

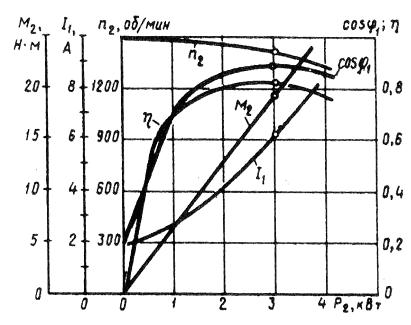
米。一、感應電動機的運行特點

依賴性 M2 = f (P2)。異步電機 M2 軸的有用扭矩對有用功率 P2 的依賴性由表達式 M2 = P2 / ω2 = 60 P2 / (2πn2) = 9.55P2 / n2 確定，

式中 P2——有用功率，W； ω2 = 2πf 2/60 是轉子的旋轉角頻率。

從這個表達式可以得出，如果 n2 = const，則圖形 M2 = f2 (P2) 是一條直線。但是在負載 P2 增加的感應電動機中，轉子的速度降低，因此軸 M2 的有用力矩隨著負載的增加增加得比負載快一點，因此圖 M2 = f (P2 ) 具有曲線形狀。

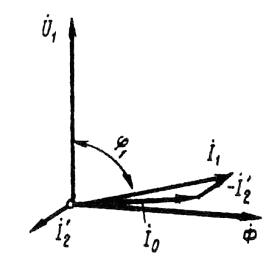
米。 2. 低負載感應電動機矢量圖

依賴性 cos φ1 = f (P2)。由於感應電機的定子電流 I1 具有在定子中產生磁場所必需的無功（感性）分量，因此感應電機的功率因數小於 1。功率因數的最低值對應於空轉。這是因為電動機的無功電流 I0 在任何負載下幾乎保持不變。因此，在低電機負載下，定子電流較小且無功（I1 ≈ I0）。因此，定子電流相對於電壓的相移很大 (φ1 ≈ φ0)，僅略小於 90°（圖 2）。

感應電動機的空載功率因數通常小於0.2。隨著電機軸上負載的增加，電流 I1 的有功分量增加，功率因數增加，在接近標稱負載時達到最高值 (0.80 — 0.90)。電機軸上負載的進一步增加伴隨著 cos φ1 的減小，這可以解釋為由於轉差增加導致轉子的感應電阻 (x2s) 增加，因此頻率增加轉子中的電流。

為了提高感應電機的功率因數，電機始終或至少大部分時間以接近額定負載的負載運行是極其重要的。這只能通過正確選擇發動機功率來實現。如果電機在大部分時間都在負載下運行，那麼要增加 cos φ1，建議降低提供給電機的電壓 U1。例如，在定子繞組為三角形連接的電機中，這可以通過重新連接星形定子繞組來實現，這將導致相電壓降低一個係數。在這種情況下，定子磁通量以及勵磁電流都會降低大約一個因子。此外，定子電流的有功分量略有增加。所有這些都有助於提高發動機的功率因數。

在圖。圖 3 顯示了當定子繞組以星形（曲線 1）和三角形（曲線 2）連接時，異步電動機 cos φ1 對負載的依賴關係圖。

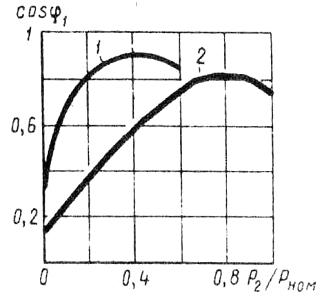
米。 3. 電機定子繞組採用星形（1）和三角形（2）連接時，cos φ1 對負載的依賴性