磁路計算

在電機和設備中，磁通量 F 集中在磁路（鐵磁芯）和該磁路的氣隙中。這條磁通路徑稱為磁路。

磁路就像電路。磁通量 Ф 類似於電流 I，感應 В 類似於電流密度，磁化力 (ns) Fн (H ∙ l = I ∙ ω) 對應於 e。 ETC。和

在最簡單的情況下，磁路處處具有相同的橫截面並且由均質磁性材料製成。確定 n。 l ∙ ω 需要提供所需的感應 B，相應的強度 H 由磁化曲線確定並乘以磁場線 l 的平均長度： H ∙ l = I ∙ ω = Fm。

由此確定所需的電流 I 或線圈的匝數 ω。

複雜的磁路通常具有不同截面和磁性材料的截面。這些部分通常串聯連接，因此相同的磁通量 F 通過它們中的每一個。每個部分的感應 B 取決於該部分的橫截面，並通過公式 B = Φ∶S 分別計算每個部分。

對於不同的感應值，強度H由磁化曲線乘以電路相應部分電源線的平均長度確定。總結個人作品，得到完整的n。 c. 磁路：

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … 這決定了磁化電流或線圈匝數。

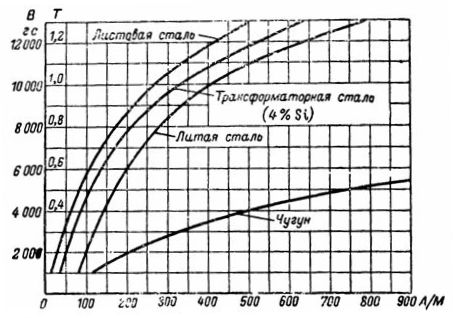
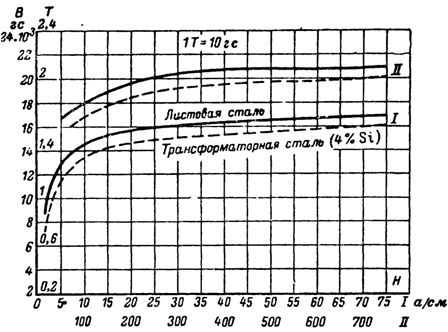
磁化曲線

示例

1. 200 匝線圈的磁化電流 I 必須是多少，以便 n。 c.在鑄鐵環上產生磁通量Ф=15700 Ms=0.000157 Wb？鑄鐵環的平均半徑為 r = 5 cm，截面直徑為 d = 2 cm（圖 1）。

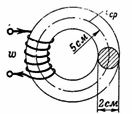
米。 1.

磁路截面 S = (π ∙ d^2) / 4 = 3.14 cm2。

鐵心感應為：B = Φ∶S = 15700∶3.14 = 5000 G。

在 MKSA 系統中，感應為：B = 0.000157 Wb：0.0000314 m2 = 0.5 T。

從鑄鐵的磁化曲線，我們發現對於B = 5000 G = 0.5 T，所需的強度H等於750 A / m。磁化強度等於：I ∙ ω = H ∙ l = 235.5 Av。

因此，所需電流 I = (H ∙ l) / ω = 235.5 / 200 = 1.17 A。

2.閉合磁路（圖2）由變壓器的鋼板製成。電流為 0.5 A 的線圈必須有多少圈才能在鐵芯中產生 Ø = 160000 Ms = 0.0016 Wb 的磁通量？

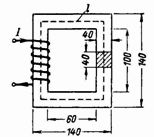
米。 2.

核心部分 S = 4 ∙ 4 = 16 cm2 = 0.0016 m2。

磁芯感應 B = F / S = 160000/16 = 10000 Gs = 1 T。

根據變壓器鋼的磁化曲線，我們發現對於 B = 10,000 Gs = 1 T，強度 H = 3.25 A / cm = 325 A / m。

磁力線的平均長度為 l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 m。

磁化力 Fm = I ∙ ω = H ∙ l = 3.25 ∙ 48 = 315 ∙ 0.48 = 156 Av。

在 0.5 A 的電流下，匝數為 ω = 156 / 0.5 = 312。

3.磁路如圖所示。圖 3 類似於前面示例的磁路，只是它具有 δ = 5 mm 的氣隙。應該是什麼。 s. 和線圈電流，使磁通量與前面的例子相同，即 F = 160000 Ms = 0.0016 Wb？

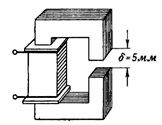
米。 3.

磁路有兩個串聯部分，其橫截面與前面示例中的相同，即 S = 16 cm2。電感也等於 B = 10000 G = 1 T。

鋼磁力線平均長度略短：lс=48-0.5=47.5cm≈0.48m。

該段磁路的磁電壓為Hc ∙ lc = 3.25 ∙ 48≈156 Av。

氣隙中的場強為：Hδ = 0.8 ∙ B = 0.8 ∙ 10000 = 8000 A / cm。

氣隙橫截面中的磁張力 Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av。

完成 n。 c. 等於各個部分的磁電壓總和：I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av。 I = (I ∙ ω) / ω = 4156/312 = 13.3 A。

如果在前面的示例中所需的磁通量由 0.5 A 的電流提供，那麼對於氣隙為 0.5 cm 的磁路，需要 13 A 的電流才能獲得相同的磁通量。由此可見，氣隙，即使相對於磁路的長度而言微不足道，也會大大增加所需的 n。 v. 和線圈電流。

4、變壓器的磁通計算為F = 72000 Ms。需要計算 n。s. 和具有 800 匝的初級繞組的磁化電流。變壓器鐵心有間隙δ=0.2mm。變壓器鐵心的尺寸如圖 1 所示。 4. 鐵芯截面S = 2 ∙ 3 = 6 cm2（這種形狀的鐵芯變壓器稱為鎧裝）。

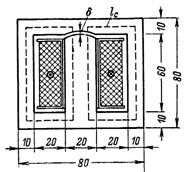
米。 4.

磁芯和氣隙感應 B = F / S = 72000/6 = 12000 G。

根據B=12000G變壓器鋼的磁化曲線，我們確定強度：Hc=5A/cm。

鋼中磁力線的平均長度為 lс = 2 ∙ (6 + 3) = 18 cm。

氣隙中的電壓 Hδ = 0.8 ∙ B = 9600 A / cm。

磁化力 I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0.02 = 90 + 192 = 282 Av； I = (I ∙ ω) / ω = 282/800 = 0.35 A。

在鎧裝鐵芯中，磁通分成兩部分，沿側桿閉合，側桿截面為S/2，磁力線平均長度為lc。結果，磁路完全類似於具有公共鐵芯S和電力線長度lc的常規變壓器的磁路。

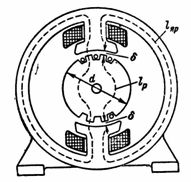
5、直流電機的磁通量F=1280000 Mks。磁路包含一個平均磁力線長度 lа = 80 cm 的鑄鋼磁軛，一個由電工鋼板組裝而成的轉子，平均磁場長度 lр = 18 cm，以及兩個氣隙 δ 0.2 cm。 = 8 ∙ 20 平方厘米；轉子和磁極截面 Sр = 12 ∙ 20 cm2... 計算 n。 p. 和磁極線圈的匝數，如果其中的最大磁化（勵磁）電流為 1 A（圖 5）。

米。 5.

磁軛和磁極中的感應 Bя = Ф / Sя = 1280000/160 = 8000 G。

根據 Bя = 8000 G 的鑄鋼磁化曲線，磁軛和磁極中的電壓等於：

H = 2.8 安/厘米。

磁軛部分的磁化力 HЯ∙la = 2.8∙80 = 224 Av。

轉子、磁極和氣隙中的感應 Br = Ф / Ср = 1280000/240 = 5333 G。

由鋼板製成的轉子中的電壓 Br = 5333 Gs Hrp = 0.9 A / cm，

轉子部分的磁電壓 Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av。

氣隙中的電壓 Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A / cm。

氣隙橫截面的磁電壓 Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 A。

完成 n。 c. 等於各部分磁電壓之和：I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ； I ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 平均值。

二極線圈匝數ω=(I∙ω)/I=1946.76/1≈2000。