電力線的電阻、電導和等效電路

電源線具有沿其長度均勻分佈的有源電阻和電感電阻以及有源電導和電容電導。

在電力傳輸網絡的實際電氣計算中，通常用常數組合代替均勻分佈的直流線路：有源 r 和電感 x 電阻以及有源 g 和電容 b 電導率。對應於這種情況的U型線的等效電路如圖1所示。 1，一個。

在計算電壓為 35 kV 且電導率 g 和 b 以下的本地輸電網絡時，可以忽略並使用由串聯連接的有源電阻和電感電阻組成的更簡單的等效電路（圖 1，b）。

線性電阻由公式確定

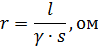
式中 l 為導線長度，m； s為電線或電纜線芯的截面，mmg γ為材料的具體設計電導率，m/ohm-mm2。

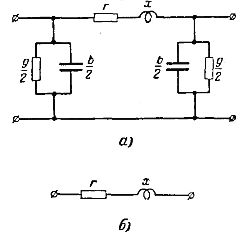
米。 1.換線方案：a——針對區域輸電網； b——本地電力傳輸網絡。

單芯和多芯線在20°C溫度下的比電導率的平均計算值，考慮到它們的實際橫截面和多芯線絞合時增加的長度，為53米/歐姆∙ mm2 用於銅，32 m / ohm ∙ mm2 用於鋁。

鋼絲的有效電阻不是恆定的。隨著通過導線的電流增加，表面效應增加，因此導線的有效電阻增加。鋼絲的有效電阻由實驗曲線或表格確定，取決於流過它們的電流值。

線路感性電阻。如果將三相電流線重新排列（換位），則在頻率為50 Hz時，線長1 km的相感應電阻可由公式確定

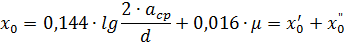
其中： asr 是線軸之間的幾何平均距離

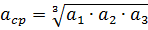
a1、a2、a3為各相導線軸線間距，d為導線外徑按導線GOST表取； μ為金屬導體的相對磁導率；對於有色金屬線材，μ = 1； x'0——由於導體外部的磁通量引起的線路外感電阻； x «0 — 由於在導體內部閉合的磁通量，線路的內部感應電阻。

每線長電感電阻 l km

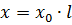
具有有色金屬導體的架空線的感應電阻 x0 平均為 0.33-0.42 歐姆/公里。

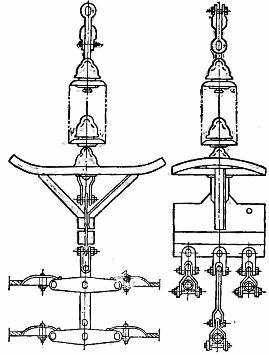
電壓為 330-500 kV 以減少電暈損耗的線路（見下文）不是使用一個大直徑的芯線，而是每相使用兩個或三個鋼鋁導體，彼此之間的距離很短。在這種情況下，線路的感應電阻會顯著降低。在圖。圖2為500kV線路上相的類似實現，三根導線位於邊長為40cm的等邊三角形的頂點處，相導線在截面上用若干剛性條紋固定。

每相使用多根導線相當於增加導線的直徑，從而導致線路的感應電阻降低。後者可以使用第二個公式計算，將其右側的第二項除以 n，並用公式確定的等效直徑 de 代替導線的外徑 d

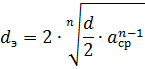
式中 n——線路一相的導線數； acp——一相導體間的幾何平均距離。

每相使用兩根電線，線路的感應電阻降低約 15-20%，使用三根電線 - 降低 25-30%。

相導體的總橫截面等於所需的設計橫截面，後者無論如何分為兩個或三個導體，這就是為什麼這種線路通常被稱為分裂導線。

鋼絲具有更大的 x0 值，因為 磁導率 變得大於 1，第二個公式的第二項是決定性的，即內部感應電阻 x «0。

米。 2、500平米單相三分線掛花環。

由於鋼的磁導率依賴於流過鋼絲的電流值，因此很難從鋼絲中確定 x « 0。因此，在實際計算中，鋼絲的x»0是根據實驗得到的曲線或表格來確定的。

三芯電纜的感應電阻可按以下平均值取：

• 對於三線電纜 35 kV — 0.12 ohms / km

• 對於三線電纜 3-10 kv-0.07-0.03 歐姆/公里

• 用於高達 1 kV-0.06-0.07 ohms / km 的三線電纜

有源導線由其電介質中的有源功率損耗定義。

在所有電壓的架空線路中，即使在空氣污染嚴重的地區，通過絕緣體的損耗也很小，因此不予考慮。

在電壓為 110 kV 及以上的架空線路中，在某些條件下，由於電線周圍空氣的強烈電離並伴有紫光和特徵性爆裂聲，電線上會出現電暈。電線冠在潮濕天氣下特別強烈。減少電暈功率損失的最根本方法是增加導體的直徑，因為隨著導體直徑的增加，電場強度以及導體附近空氣的電離度都會降低。

對於 110 kV 線路，電暈條件下的導體直徑應至少為 10-11 mm（導體 AC-50 和 M-70），對於 154 kV 線路 - 至少為 14 mm（導體 AC-95），以及對於 220 kV 線路——不小於 22 mm（導體 AC -240）。

110-220 kV 架空線路在規定的和大導線直徑的導線中電暈的有功功率損耗是微不足道的（每 1 公里線路長度數十千瓦），因此在計算中不考慮它們。

在330和500kV線路中，每相使用兩根或三根導線，如前所述，相當於增加了導線的直徑，其結果是導線附近的電場強度顯著增加減少，導體有輕微腐蝕。

在 35 kV 及以下的電纜線路中，電介質中的功率損耗很小，也未考慮在內。在電壓為 110 kV 或更高的電纜線路中，每 1 km 長度的介電損耗達到幾千瓦。

由於導體之間以及導體與地之間的電容而導致線路的電容性傳導。

三相架空線路的容性電導在滿足實際計算精度的情況下可由下式確定

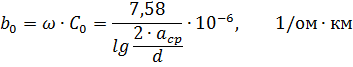
其中 C0 為線路的工作容量； ω——交流電的角頻率； acp 和 d — 見上文。

在這種情況下，不考慮土壤的電導率和電流返回地面的深度，並假設導體沿線路重新排列。

對於電纜，工作容量根據出廠數據確定。

線性電導率 l km

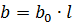
線路中電容的存在導致電容電流流動。電容電流超前相應相電壓 90°。

在具有沿長度均勻分佈的恆定電容電流的實際線路中，電容電流沿線路長度不均勻，因為線路兩端的電壓大小不恒定。

接受直流電壓的線路始端的電容電流

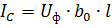
其中 Uph 是線相電壓。

電容線路電源（線路產生的功率）

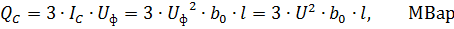
其中 U 是相間電壓，sq。

從第三個公式可以看出，線路的電容電導率幾乎不依賴於導體之間的距離和導體的直徑。線路產生的功率高度依賴於線路電壓。對於 35 kV 及以下的架空線路，它非常小。對於長度為 100 km 的 110 kV 線路，Qc≈3 Mvar。對於長度為 100 km 的 220 kV 線路，Qc≈13 Mvar。拆分電線會增加線路容量。

僅在 20 kV 及以上的電壓下才考慮電纜網絡的電容電流。