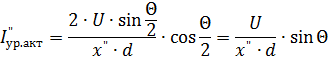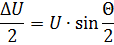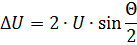發電機並聯運行

在發電廠中，總是安裝多個渦輪或液壓單元，它們在發電機或浪湧的公共母線上並聯工作。

因此，發電廠的電力生產是由多台發電機並聯工作產生的，這種合作具有許多寶貴的優勢。

發電機並聯運行：

1.增加了發電廠和變電站設備運行的靈活性，便於發電機、主設備和相應配電設備的預防性維護，所需的儲備最少。

2. 提高發電廠的運行效率，因為它可以在機組之間最有效地分配每日負荷計劃，從而實現電力的最佳利用並提高效率；在水力發電廠中，可以在洪水期和夏季和冬季枯水期最大限度地利用水流的力量；

3.提高發電廠和消費者供電的可靠性和不間斷運行。

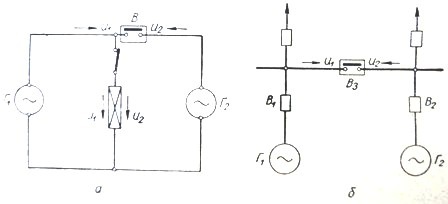
米。 1、發電機並聯運行示意圖

為了提高產量和改善配電，將許多發電廠聯合起來並聯運行，形成強大的電力系統。

在正常運行中，發電機連接到公共母線（發電機或過電壓）並同步旋轉。它們的轉子以相同的電角速度旋轉

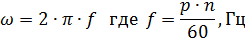
並聯運行時，兩台發電機兩端的瞬時電壓必須大小相等，符號相反。

要將發電機與另一台發電機（或網絡）並聯運行，必須對其進行同步，即根據運行的發電機調節所連接發電機的旋轉速度和勵磁速度。

並聯運行和連接的發電機必須同相，即具有相同的相位旋轉順序。

從圖中可以看出。 1、並聯運行時，發電機之間是相對連接的，即它們在開關上的電壓U1和U2正好相反。相對於負載，發電機是一致工作的，即它們的電壓U1和U2相匹配。發電機並聯運行的這些條件反映在圖 1 的圖表中。 2.

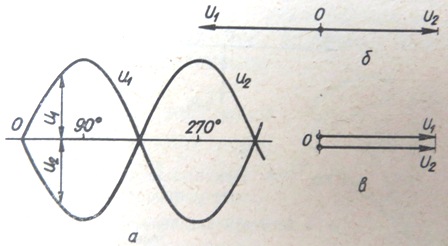
米。 2.發電機並聯運行的條件。發電機電壓大小相等，相位相反。

同步發電機有兩種方法：精同步和粗同步或自同步。

發電機精確同步的條件。

通過精確同步，勵磁發電機在達到同步條件後通過開關 B（圖 1）連接到網絡（母線）——它們的電壓瞬時值 U1 = U2 相等

當發電機單獨運行時，它們的瞬時相電壓將分別相等：

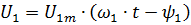
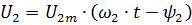
這意味著發電機並聯所需的條件。對於啟動和運行的發電機，需要：

1.有效電壓值相等U1 = U2

2.角頻率相等ω1=ω2或f1=f2

3. 相位 ψ1 = ψ2 或 Θ = ψ1 -ψ2 = 0 的電壓匹配。

準確滿足這些要求創造了理想條件，其特徵在於在發電機接通時，定子均衡電流將為零。然而，應該注意的是，要滿足精確同步的條件，需要仔細調整髮電機電壓的電壓、頻率和相位角的比較值。

在這方面，完全滿足同步的理想條件實際上是不可能的；它們是近似執行的，有一些細微的偏差。如果不滿足上述條件之一，當U2時，電壓差將作用在斷開的通訊開關B的端子上：

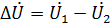
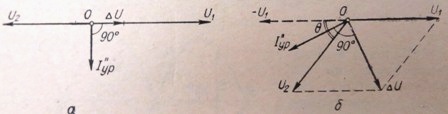
米。 3.偏離精確同步條件的情況的矢量圖： a——發電機工作電壓不相等； b——角頻率不相等。

當開關導通時，在該電位差的作用下，電路中會流過均衡電流，其初始時刻的周期分量為

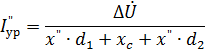
考慮兩種偏離圖中所示的精確同步條件的情況（圖 3）：

1、發電機U1、U2的工作電壓不相等，其他條件都滿足；

2、發電機電壓相同，轉速不同，即角頻率ω1和ω2不相等，電壓相位不匹配。

從圖中的圖表可以看出。 3、a、電壓U1和U2的有效值\u200b\u200b不等導致出現均衡電流I”ur，這幾乎是純感性的，因為發電機和連接線的有源電阻網絡非常小，被忽視了。該電流不會產生有功功率浪湧，因此不會在發電機和渦輪機部件中產生機械應力。在這方面，當發電機並聯運行時，電壓差最多允許 5-10%，在緊急情況下最多允許 20%。

當均方根電壓值 U1 = U2 相等，但角頻率不同 Δω = ω1 — ω2 ≠ 0 或 Δf = f1 — f2 ≠ 0 時，發電機和網絡（或第 2 台發電機）的電壓矢量) 以隨時間變化的特定角度 θ 移動。在這種情況下，發電機 U1 和 U2 的電壓相位將不會相差 180°，而是相差 180° —θ（圖 3，b）。

在打開的開關 B 的端子處，a 點和 b 點之間，電壓差 ΔU 將起作用。與前面的情況一樣，可以使用燈泡檢測電壓的存在，並且可以使用連接在 a 點和 b 點之間的電壓表測量該電壓的有效值。

如果開關 B 閉合，則在電壓差 ΔU 的作用下，會出現均衡電流 I”，與 U2 相關的電流幾乎是純活動的，當發電機並聯時，會引起衝擊和機械發電機和渦輪機的軸和其他部件中的應力。

在 ω1 ≠ ω2 時，如果滑差為 s0 < 0, l% 且角度 Θ ≥ 10°，則同步完全令人滿意。

由於渦輪調節器的慣性，不可能實現角頻率 ω1 = ω2 和電壓矢量之間的角度 θ 的長期相等，表徵發電機定子和轉子繞組的相對位置，不會保持不變，而是不斷變化；它的瞬時值為 Θ = Δωt。

在矢量圖（圖 4）中，最後一種情況將表示為隨著電壓矢量 U1 和 U2 之間的相位角的變化，ΔU 也將發生變化。此時的電壓差ΔU稱為衝擊電壓。

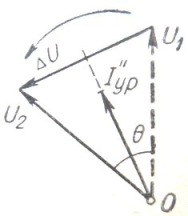
米。 4.頻率不等的發電機同步矢量圖。

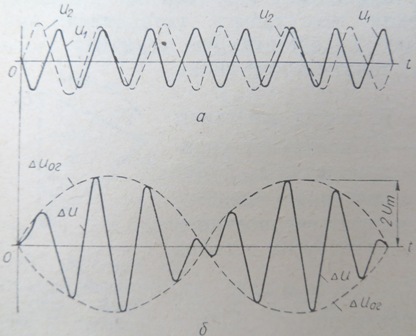
時鐘電壓的瞬時值 Δu 是發電機電壓 u1 和 u2 的瞬時值之差（圖 5）。

假設達到有效值U1 = U2相等，則參考時刻ψ1和ψ2的相位角也相等。

然後你可以寫

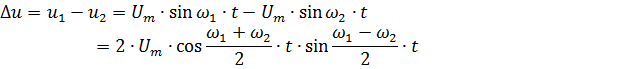
衝擊應力曲線如圖 1 所示。 5.

節奏電壓諧波變化，其頻率等於比較頻率總和的一半，幅度隨時間變化，具體取決於相位角 Θ：

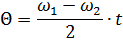
從圖中的矢量圖。4、對於某一規定的角度θ值，可求出衝擊應力的有效值：

米。 5.克服壓力的曲線。

考慮到角度 θ 隨時間的變化，可以根據衝擊應力振幅寫出殼的表達式，它給出了應力振幅隨時間的變化（圖 5，b 中的虛線曲線） ):

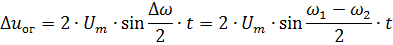
從圖中的矢量圖可以看出。 4和最後一個方程，衝擊應力幅值ΔU從0到2 Um變化。 ΔU 的最大值出現在電壓矢量 U1 和 U2（圖 4）相位和角度 θ = π 重合的時刻，最小值出現在這些電壓的相位相差 180° 且角度 θ = 0 時。節奏曲線的周期等於

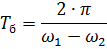
當發電機與大功率系統並聯運行時，系統的xc值很小，可以忽略不計（xc≈0），則均衡電流

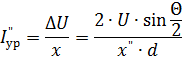
和浪湧電流

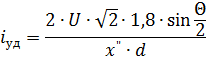
在電流Θ = π 不利合閘的情況下，合閘發電機定子繞組中的浪湧電流可達到發電機端子三相短路浪湧電壓值的兩倍。

均衡電流的有源分量，從圖 1 中的矢量圖可以看出。 4等於