連續振盪和參數共振

連續振動——能量不隨時間變化的振動。在真實的物理系統中，總會有一些原因導致振動能向熱能的轉變（例如機械系統中的摩擦，電氣系統中的主動電阻）。

因此，只有補充這些能量損失才能獲得無阻尼振盪。由於來自外部源的能量，這種補充在自振盪系統中自動發生。連續電磁振蕩的應用極為廣泛。使用不同的生成器來獲取它們。

為了使（擺動圓或擺的）電氣或機械振動不受阻尼，必須始終補償阻力或摩擦損失。

例如，您可以使用交變 EMF 作用於振盪電路，這將周期性地增加線圈中的電流，並相應地保持電容器中的電壓幅度。或者您可以用類似的方式推動鐘擺，使其保持和諧擺動。

大家知道，振盪電路線圈的磁場能量的大小與其電感量和電流有如下關係（第二式為電容器電場的能量 相同的輪廓輪廓）

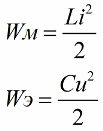
從第一個公式可以清楚地看出，如果我們週期性地增加線圈中的電流，作用於交變 EMF 電路，那麼（通過增加或減少公式中的第二個因素——電流）我們將周期性地為該電路補充能量。

嚴格按電路的自然自由振盪時間，即在諧振頻率作用於電路，我們會得到電諧振現象，因為它在諧振頻率 振盪系統 最集中地吸收提供給它的能量。

但是，如果您不定期更改第二個因素（不是電流或電壓），而是第一個因素 - 電感或電容，會怎樣？在這種情況下，電路的能量也會發生變化。

例如，定期將磁芯推入和推出線圈或推入和推出電容器電介質, — 我們還得到電路中能量的非常明確的周期性變化。

我們為線圈電感的單位變化寫下這個位置：

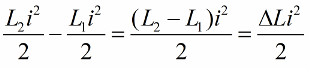
電路擺動的最顯著影響是及時改變電感。例如，如果我們在任何時刻採用相同的電路，當一些電流 i 已經流過它時，將一個磁芯引入線圈，那麼能量將改變如下：

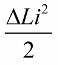
現在讓電路本身出現自由振盪，但是在四分之一周期後能量完全傳遞到電容器並且線圈中的電流變為零的那一刻，我們將突然從線圈中取出磁芯電感將恢復到其原始狀態，即初始值 L。當磁芯被移除時，不需要對磁場做任何功。因此，當鐵芯被推入線圈時，電路接收到能量，因為我們工作了，其值：

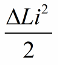
四分之一周期後，電容開始放電，其能量再次轉化為線圈磁場的能量，當磁場達到一定幅度時，我們將再次對鐵芯進行猛烈的擠壓。電感再次增加，增加了相同的量。

同樣，在零電流下，我們將電感返回到其原始值。這樣一來，如果每半個週期的能量增益超過電阻損耗，則迴路的能量會一直增加，振盪幅度也會增加。這種情況由不等式表示：

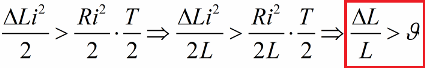
在這裡，我們將這個不等式的兩邊除以 L，並寫下對數遞減的特定值通過跳躍進行參數激勵的可能性的條件。

建議每個週期更改電感（或電容）兩次，因此參數更改的頻率（參數諧振頻率）應為振盪系統固有頻率的兩倍：

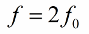
於是電路中的振盪激勵路徑就出現了，不需要直接改變電動勢或電流。電路中的初始波動電流總是以這種或另一種方式存在，這甚至沒有考慮大氣中射頻振蕩的干擾。

如果電感（或電容）沒有跳躍變化，而是諧波變化，那麼振盪發生的條件看起來會有點不同：

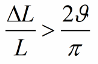
由於電容和電感是電路參數（如鐘擺的質量或彈簧的彈性），因此激勵振蕩的方法也稱為參數激勵。

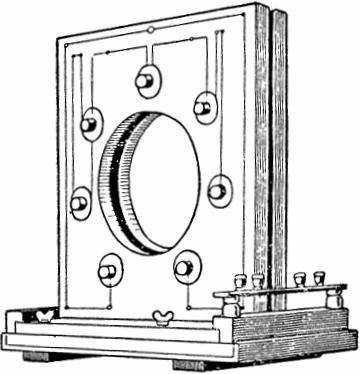
這一現像在20世紀初被蘇聯物理學家曼德爾施塔姆和帕帕列西發現並進行了實踐研究。基於這一物理現象，他們建造了第一台功率為4千瓦、可變電感的參量交流發電機。

在發電機的設計中，七對扁平線圈位於框架的兩側，在其空腔中有一個帶有突起的鐵磁性圓盤旋轉。當圓盤被電機驅動旋轉時，其突起週期性地進出每對線圈之間的空間，從而改變電感並激發振盪。