電氣工程和電子學中的振盪過程,振盪類型
振盪過程——具有不同程度可重複性的過程。所有振盪過程分為兩類:週期性和非週期性。理論上,他們還使用中間類——幾乎是周期性的振盪。
振盪過程稱為周期性的,其中表徵此過程的值在特定時間段 T 後的任何時間取值具有相同的值。
函數 f (t) 是振盪過程的數學表達式,如果滿足條件 f (t + T) = f (t),則稱為周期為 T 的周期函數。
在一類週期性振盪過程中,諧波振盪或正弦振蕩起著主要作用,其中物理量隨時間的變化根據正弦或餘弦定律發生。他們的總記錄是:
y = f (t) = aCos ((2π / T) t — φ),
其中 a — 振盪幅度,φ 是振盪相位,1 /T = f — 頻率和 2πf = ω — 循環或圓形振動的頻率。
正弦振蕩的應用及其特點:
對應於週期性振盪讀數的幾乎週期性函數由以下條件定義:
| f · (t + τ) — f (t) | <= ε 其中 ε — 為每個值 T 分配一個值。
這種情況下的量 τ 稱為幾乎週期。如果 ε 的值與時間 T 處的 f (t) 的平均值相比非常小,則準週期函數將接近週期函數。
非週期性振盪比周期性振盪變化多端。但在自動化中,最常見的情況是必須滿足阻尼或增加正弦振蕩的要求。
根據阻尼正弦波定律的振盪,或有時稱為阻尼諧波振盪,可以用一般形式表示:
x = Ae-δTcos·(ω + φ),
其中 t 是時間,A 和 φ 是任意常數。增加諧波振盪定律的一般表示法僅在阻尼因子 δ[1 秒] 的符號上有所不同。
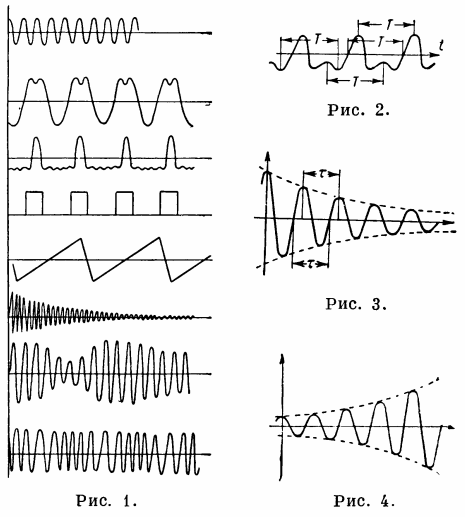
如圖。 1 - 振盪過程,圖。 2. - 週期性過程,圖。 3. - 衰減諧波振盪,圖。 4. — 諧波振盪增加。
振盪過程的一個應用例子是最簡單的振盪電路。
振盪器電路(電路)— 一種無源電路,其中可以以由電路本身的參數確定的頻率發生電振盪。
最簡單的振盪電路由電容 C 和電感 L 組成。在沒有外部影響的情況下,頻率為 εО = 1/2π√LC 的阻尼振盪。
振動的幅度隨 eg-δT 減小,其中 δ 是阻尼係數。如果 δ> = eO,則電路中的阻尼振盪變為非週期性。
在電子學中,振盪電路的好壞是由品質因數決定的:Q=nf/δ……當有外來的周期性力作用於振盪電路時,它就會發生強迫振盪。如果外部影響的頻率接近 eo(共振),則高 Q 電路的受迫振盪幅度會顯著增加。振盪電路是諧振放大器中的主要部件之一, 發電機 和其他電子設備。
另請參閱此主題: 電壓諧振和電流諧振的應用
