電路的時間常數——它是什麼以及用在什麼地方

週期性過程是自然界固有的：白天之後是夜晚，暖季被寒冷取代等。這些事件的周期幾乎是恆定的，因此可以嚴格確定。此外，我們有權聲稱，作為示例引用的周期性自然過程不會貶值，至少就人的壽命而言是這樣。

然而，在技術領域，尤其是在電氣工程和電子領域，並非所有過程都是周期性的和連續的。通常，一些電磁過程先增大後減小。通常物質只限於振蕩的開始階段，沒有時間真正加快速度。

在電氣工程中，您經常會發現所謂的指數瞬態，其本質是系統只是努力達到某種平衡狀態，最終看起來像靜止狀態。這種轉變可以增加或減少。

外力首先使動力系統失去平衡，而後又不妨礙該系統自然恢復到原來的狀態。最後一個階段是所謂的過渡過程，其特點是有一定的持續時間。此外，系統失衡的過程也是一個具有特徵持續時間的瞬態過程。

無論如何，暫態過程的時間常數，我們稱之為它的時間特性，它決定了這個過程的某個參數將在多少時間後變化時間«e»，即它會增加或減少約2.718倍與初始狀態相比。

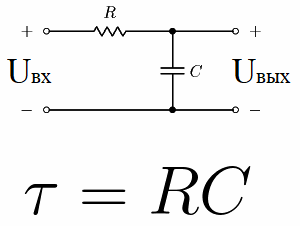
例如，考慮一個由直流電壓源、電容器和電阻器組成的電路。這種電阻與電容串聯的電路稱為RC積分電路。

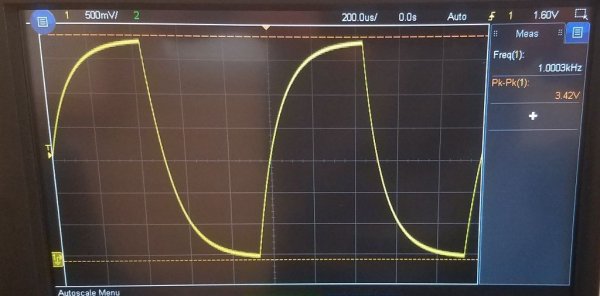
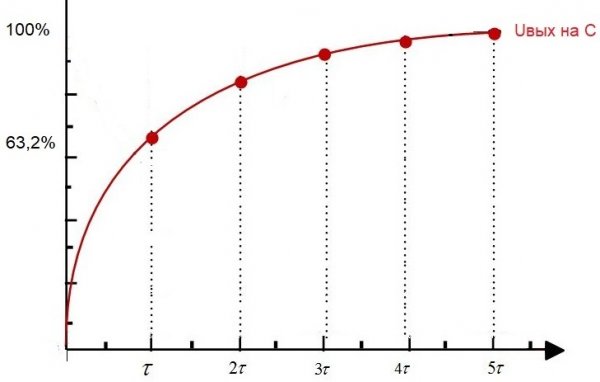
如果在初始時刻為這樣的電路供電，即在輸入端設置恆定電壓 Uin，則 Uout——電容器中的電壓將開始呈指數增長。

在時間 t1 之後，電容器電壓將達到輸入電壓的 63.2%。所以，從初始時刻到t1的時間間隔就是這個RC電路的時間常數。

該鏈常數稱為“tau”，以秒為單位，並由相應的希臘字母表示。在數值上，對於 RC 電路，它等於 R * C，其中 R 的單位是歐姆，C 的單位是法拉。

當必須切斷（抑制）較高頻率並必須通過較低頻率時，集成 RC 電路在電子設備中用作低通濾波器。

實際上，這種過濾的機制是基於以下原則。對於交流電，電容器充當容性電阻，其值與頻率成反比，即頻率越高，電容器的電抗（歐姆）越低。

因此，如果交流電通過 RC 電路，那麼，就像在分壓器的臂上一樣，電容器兩端會下降一定的電壓，與通過的電流頻率下的電容成正比。

如果已知輸入交變信號的截止頻率和幅值，那麼設計者在RC電路中選擇這樣的電容和電阻就不難了，使得最小（截止）電壓（對於截止頻率 - 頻率的上限）落在電容器上，因為電抗與電阻器一起進入分壓器。

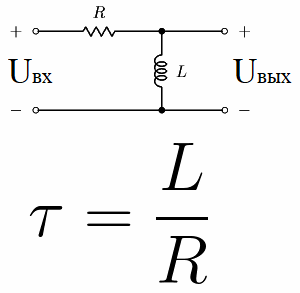
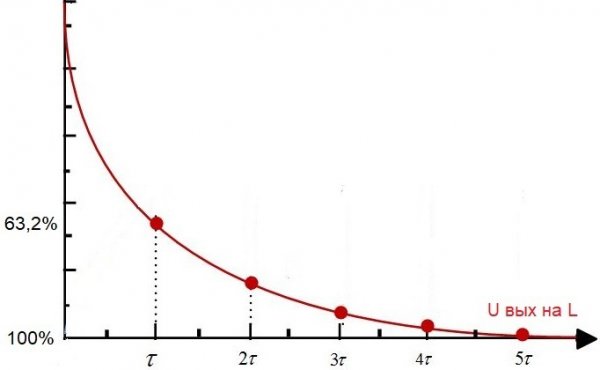
現在考慮所謂的微分電路。它是由一個電阻和一個電感串聯組成的電路，RL電路。它的時間常數在數值上等於 L / R，其中 L 是以亨利為單位的線圈電感，R 是以歐姆為單位的電阻器的電阻。

如果將來自電源的恆定電壓施加到此類電路，經過一段時間 tau 後，線圈電壓將相對於 U in 降低 63.2%，即完全符合該電路的時間常數值.

在 AC 電路（交流信號）中，當必須切斷（抑制）低頻並且忽略高於（高於截止頻率 - 頻率下限）的頻率時，LR 電路用作高通濾波器。所以，線圈的電感越大，頻率就越高。

與上面討論的 RC 電路的情況一樣，這裡使用分壓器原理。通過 RL 電路的更高頻率的電流將導致電感 L 上的電壓降更大，就像作為分壓器和電阻器的一部分的電感電阻一樣。設計者的任務是選擇這樣的 R 和 L，以便恰好在邊界頻率處獲得線圈的最小（邊界）電壓。