變壓器效率

變壓器的效率取決於變壓器輸送給負載的功率 P2 與網絡消耗的功率 P1 的比值：

η = P2 / P1

效率表徵變壓器中電壓轉換的效率。

在實際計算中，變壓器的效率由下式計算

η = 1 — (∑P — (P2 + ∑P),

其中 ∑P = Pmail + Pmg — 變壓器的總損耗。

該公式對 P1 和 P2 的確定誤差不太敏感，因此可以獲得更準確的效率值。

變壓器輸送到網絡的淨功率由下式計算

P2 = m NS U2n NS I2n NS kng NS Cosφ2 = kng NS Сn NS Cosφ2,

其中 kng = I2 / I2n — 變壓器的負載係數。

繞組中的電損耗由變壓器的短路經歷決定。

Pmail = kng2 NS P是的，

其中 Pk = rk x I21n — 額定電流下的短路損耗。

鋼材中的損耗Rmg由怠速試驗確定 rmg = Ro

假設它們對於變壓器的所有操作模式都是恆定的，因為當 u1 = const EMF E1 時，操作模式中的 E1 變化不顯著。

綜上所述，變壓器的效率可由下式確定：

η = (Po + kng2 NS PSe) / (kng NS Сn NS Cosφ2 + Po + kng2 NS PSe),

對該表達式的分析表明，當繞組中的損耗等於鋼中的損耗時，變壓器的效率在負載處具有最大值。

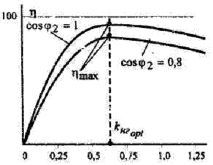
米。 1、變壓器負荷係數最佳值的確定

由此我們得到變壓器負載係數的最優值：

kngopt = √Po / P待

在現代電力變壓器中，損耗係數Po/P1=（0.25—0.4）；因此，η 的最大值出現在 kng = 0.5 — 0.6 時（圖 1）。

從η(kng)曲線可以看出，變壓器在0.5到1.0的寬負載變化範圍內具有幾乎恆定的效率。在低負載時，變壓器的 η 急劇下降。

變電站