感應電動機在不同模式、電壓和頻率下的機械特性
感應電動機的機械特性可以表示為n=f(M)或n=e(I)。然而，異步電動機的機械特性通常以依賴關係的形式表示 M = f(S)，其中 C — 滑動，S = (nc-n) / nc，其中 ns — 同步速度。
在實踐中，一個稱為 Kloss 公式的簡化公式用於機械特性的圖形構造：
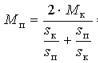
此處：Mk — 臨界（最大）扭矩值。這個力矩值對應於臨界滑移
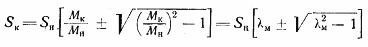
其中λm = Mk / Mn
Kloss 公式用於解決與使用感應電機執行的電力驅動相關的問題。使用 Kloss 公式，您可以根據感應電機的護照數據構建機械特性圖。在實際計算中，確定根前的臨界力矩時，公式中只需考慮加號即可。
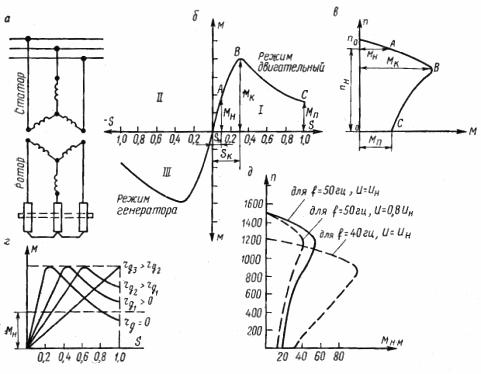
米。 1.異步電動機：a——示意圖，b——機械特性 M=f(S)——電動機和發電機模式下的自然機械特性，c——電動機模式下的自然機械特性n=f(M)，d——人工變阻器的機械特性， e——不同電壓和頻率下的機械特性。
鼠籠式感應電動機
從圖中可以看出。圖 1，位於 I 和 III 象限的感應電動機的機械特性。 I 象限中的曲線部分對應於正轉差值並表徵異步電動機的運行模式，而在 III 象限中則表徵發電機模式。發動機模式具有最大的實際意義。
電機模式的機械特性圖包含三個特徵點：A、B、C，並且可以有條件地分為兩部分：OB 和 BC（圖 1，c）。
A點對應電機的額定轉矩，由公式Mn = 9.55•103•(Strn /nn)確定
這一刻對應 標稱滑移，對於具有一般工業應用的發動機，其值在 1 至 7% 的範圍內，即 Sn = 1 — 7%。同時，小型發動機打滑較多，大型發動機打滑較少。
用於衝擊負載的高轉差電機具有 Сn~15%。這些包括，例如，單串聯交流電機。
特性曲線的 C 點對應於啟動時電機軸上出現的初始扭矩值。這個時刻 Mp 被稱為初始或開始。在這種情況下，滑移等於 1，速度為零。 啟動扭矩 從參考表的數據很容易確定，該表顯示了啟動扭矩與標稱 Mp / Mn 的比率。
在電壓和電流頻率恆定值下啟動轉矩的大小取決於轉子電路中的有源電阻。在這種情況下，最初隨著有源電阻的增加，啟動轉矩的值增加，當轉子電路的有源電阻等於電動機的總感應電阻時達到最大值。隨後，隨著轉子有功電阻的增大，初始轉矩的值減小，在極限時趨於零。
C 點（圖 1，b 和 c）對應於發動機在從 n = 0 到 n = ns 的整個轉數範圍內可以發展的最大力矩......這個力矩稱為臨界（或傾覆）力矩 Mk .臨界力矩也對應於臨界滑移Sk。臨界滑移 Sk 的值越小，標稱滑移 Сn 的值越小，機械特性的剛度就越大。
起始時刻和關鍵時刻由標稱時刻決定。根據鼠籠式電機的 GOST，必須滿足條件 Mn / Mn = 0.9 — 1.2，Mk / Mn = 1.65 — 2.5。
需要注意的是，臨界力矩的值與轉子迴路的有功電阻無關，而臨界轉差Сk與該電阻成正比。這意味著隨著轉子電路的有效電阻的增加，臨界力矩的值保持不變，但扭矩曲線的最大值向增加的轉差值移動（圖 1，d）。
臨界轉矩的大小與施加到定子上的電壓的平方成正比，與定子中電壓頻率和電流頻率的平方成反比。
例如，如果提供給電機的電壓等於額定值的 85%，則臨界轉矩的大小將為額定電壓下的 0.852 = 0.7225 = 72.25% 臨界轉矩。
改變頻率時觀察到相反的情況。例如，如果對於設計為以電流頻率 = 60 Hz 運行的電機，電源電流頻率 = 50 Hz，則臨界力矩將大於 (60/50)2=1.44 倍其頻率的官方值（圖 1，e）。
臨界力矩表徵電機的瞬時過載能力，即表示電機能夠承受多長時間（幾秒內）的過載而不產生任何有害後果。
機械特性從零到最大（臨界）值（見圖 1，biv）的部分稱為特性的穩定部分，BC 部分（圖 1，c）稱為不穩定部分。
這種劃分可以通過以下事實來解釋：在 OF 特性的增加部分，隨著滑移的增加，即隨著速度的降低，發動機產生的扭矩增加。這意味著隨著負載的增加，即隨著制動力矩的增加，電機的轉速降低，由此增加的扭矩增加。當負載減小時，反之，轉速增大，轉矩減小。隨著負載在整個特性穩定部分的範圍內變化，電機的轉速和轉矩發生變化。
電機不能產生超過臨界扭矩，如果制動力矩更大，電機必然會停止。正如他們所說，發動機翻車發生了。
U 和 I 恆定且轉子電路中沒有附加電阻的機械特性稱為自然特性（具有繞線轉子的鼠籠式感應電動機的特性，轉子電路中沒有附加電阻）。人為或變阻特性稱為與轉子電路中的附加電阻相對應的特性。
所有啟動扭矩值都不同，取決於轉子電路的有源電阻。不同大小的滑塊對應相同的標稱扭矩Mn。隨著轉子電路電阻的增加，轉差增加，因此電機的速度降低。
由於轉子電路中包含有源電阻，穩定部分的機械特性在增加轉差的方向上被拉伸，與電阻成正比。這意味著電機速度開始根據軸負載發生顯著變化，並且硬特性變得軟。