單電源無分支和分支線性電路

如果大量的無源元件連同一個e源。 ETC。 c.形成一個電路，它們的互連可以用不同的方式來完成。此類連接有以下典型方案。

元件串聯 這是最簡單的連接。通過這種連接，相同的電流流過電路的所有元件。根據這種方案，要么將電路中所有的無源元件都連接起來，然後電路將是單路無分支的（圖 1.a），要么只連接多路電路的部分元件連接的。

如果n個元件串聯，其中流過相同的電流I，則電路兩端的電壓將等於n個串聯元件的電壓降之和，即

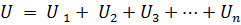
或者：

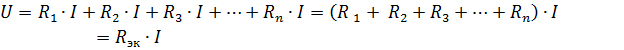
其中 Rek 是等效電路電阻。

因此，串聯連接的無源元件的等效電阻等於這些元件的電阻之和......電氣方案（圖1）1, a) 可以給出一個等效電路（圖 1, b），由一個具有等效電阻 Rek 的元件組成

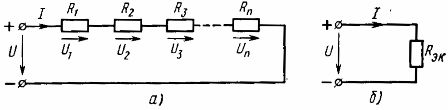
米。 1. 線性元件串聯方案(a)及其等效方案(b)

在計算具有給定電源電壓和元件電阻的元件串聯連接的電路時，電路中的電流根據歐姆定律計算：

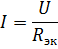
第 k 個元件上的電壓降

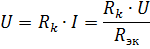
不僅取決於該元件的電阻，還取決於等效電阻Rek，即電路其他元件的電阻。這是元件串聯的一個顯著缺點。在極限情況下，當電路中任何元件的電阻變為無窮大（開路）時，電路中所有元件中的電流變為零。

由於串聯連接時，電路中所有元件中的電流相同，因此元件中的電壓降之比等於這些元件的電阻之比：

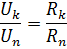
元件的並聯連接——這是一種對電路的所有元件施加相同電壓的連接。根據並聯連接方案，可以連接電路的所有無源元件（圖 2，a）或僅連接其中的一部分。每個並聯連接的元素形成一個單獨的分支。因此，如圖 1 所示的元件並聯電路。 2、a，雖然是一個簡單的電路（因為它只包含兩個節點），但它同時是有分支的。

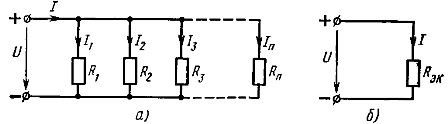
米。 2. 線性元件並聯方案(a)及其等效方案(b)

在每個並聯支路中，電流

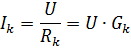
其中 Gk 是第 k 個分支的電導率。

從 基爾霍夫第一定律

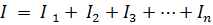
或者

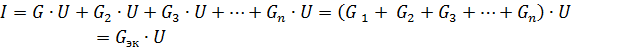
其中 Gec 是等效電路電導。

因此，當無源元件並聯時，它們的等效電導等於這些元件的電導之和……等效電導總是大於並聯支路任何部分的電導。等效電導率GEK對應於等效電阻Rek = 1 / Gek。

則得到如圖所示的等效電路。 2、a，就會有如圖所示的形式。 2、b.元件並聯電路中未支路部分的電流可由該電路根據歐姆定律求得：

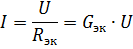
因此，如果電源電壓恆定，則隨著並聯元件數量的增加（導致等效電導率增加），電路未分支部分的電流（電源電流）增加。

從公式

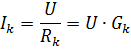
可以看出，每個支路中的電流只取決於該支路的電導，而不取決於其他支路的電導。並聯支路模式相互獨立是無源元件並聯的一個重要優點。在工業裝置中，大多數情況下使用電氣接收器的並聯連接。最明顯的例子是用於照明的電燈。

由於在並聯連接中，相同的電壓被施加到所有元件並且每個支路中的電流與該支路的電導成正比，因此並聯支路中的電流之比等於這些支路的電導之比，或成反比與它們的電阻之比：

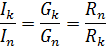
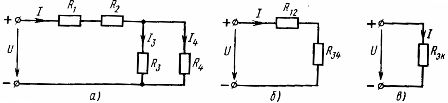
元件的混合連接是串聯和並聯連接的組合。這樣的鏈可以有不同數量的節點和分支。圖中顯示了混合連接的示例（圖 3，a）

米。 3. 線性單元混合連接方案(a)及其等價方案(b,c)。

要計算這樣的電路，必須依次確定電路中僅串聯或併聯連接的那些部分的等效電阻。在所考慮的電路中，電阻 R1 和 R2 的元件串聯連接，電阻 R3 和 R4 的元件並聯連接。利用先前獲得的電路元件參數與串聯和並聯連接之間的關係，實際電路可以依次用等效電路代替。

串聯元件的等效電阻

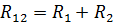
並聯元件 R3 和 R4 的等效電阻

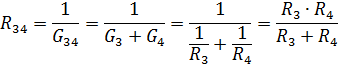
具有元件 R12 和 R34 電阻的等效電路如圖 1 所示。 3、乙。 R12和R34串聯，等效電阻為

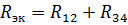
對應的等效電路如圖 1 所示。 2，乙。讓我們找出該電路中的電流：

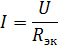
這些是實際電路的電源電流和元件 R1 和 R2 中的電流。要計算電流 I3 和 I4，請確定電阻 R34 電路部分的電壓（圖 3，b）：

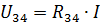
那麼電流I3和I4可以根據歐姆定律求得：

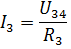
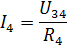
以類似的方式，您可以計算許多其他混合連接無源元件的電路。

對於具有大量電路和e源的複雜電路。 ETC。 c. 這樣的等價轉換並不總能進行。它們是通過其他方法計算的。