電路拓撲——基本概念

電路是一組設備（元件）及其連接線，電流可以通過這些連接線流動。電路的所有元件共享 在被動和主動.

有源元件將不同類型的能量（機械能、化學能、光能等）轉化為電能。在無源設備中，電能被轉換成其他類型的能量。主動元素稱為源，被動元素稱為消費者或接收者。

在電路理論中，考慮了電氣元件的理想化模型。這使得元素的描述盡可能簡單。更複雜的真實元素是根據一組理想化元素建模的。

電路中主要的無源元件有電阻器（電阻元件）、電感器（電感元件）和電容器（電容元件）。元件安裝在電路中以產生給定值和形狀的電壓和電流（參見 - 電路及其元件).

電路由分支和節點組成。 分支 — 這是流過相同電流的電路（電路）的一部分。 一個結 ——三個或更多支路的連接。在電氣圖上，節點用點表示（圖 1）。

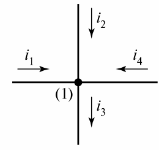
米。 1.定義圖中的節點

如有必要，圖的節點從上到下從左到右編號。

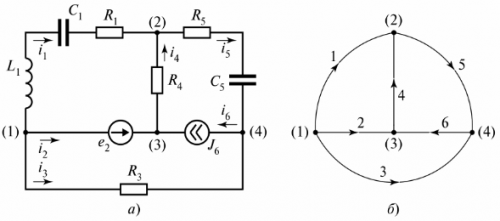
在圖。圖 2 顯示了電流 iC 流過的阻容支路。

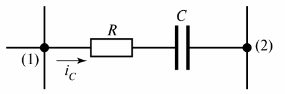
米。 2、阻容支路

可以給出分支的另一個定義——它是兩個相鄰節點（圖 2 中的節點 (1) 和 (2)）之間的電路部分。

鏈 電路中是否有閉合路徑。電路可以通過任何分支閉合，包括電阻等於無窮大的條件分支。

在圖。圖3顯示了由三個支路組成的支路電路。

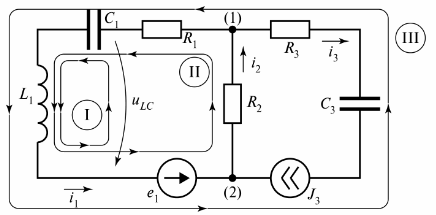
米。 3. 電路有兩個電路

該圖顯示了三個電路，電路 I 由無窮大電阻的支路閉合。該分支表示為電壓 tiLC。

對於圖一電路3 可以組成許多由實數或條件分支閉合的循環，但是為了計算電噪聲，使用了“獨立循環”的概念。獨立電路迴路的數量始終設置為計算所需的最小值。

獨立電路總是閉合的，但分支的電阻不等於無窮大，並且每個獨立電路至少包含一個不包含在其他電路中的分支。對於復雜的電路，您可以使用電路圖確定獨立電路的數量。

在電路圖上 稱為電路的條件表示，其中每個分支都由一條線段代替。不顯示分支中的項目。例如，在圖。圖 4 顯示了一個分支電路及其示意圖。

米。 4、分支電路：a——電路圖，b——圖

要製作圖表的圖表，您必須使用分支線連接節點，而無需在其上指定元素。分支被編號，它們上面的電流方向用箭頭表示。該圖本身沒有物理意義，但可以用來判斷獨立等值線的數量和類型。為此，準備了一個“圖形樹”。

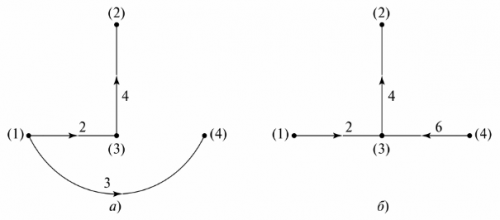
圖形樹 它表示電路圖，其節點通過分支連接，不會產生閉環。顯示圖形樹可能有幾個選項。在圖。圖5示出了圖4的電路的兩個可能選項。 4.

米。 5. 方案圖解樹

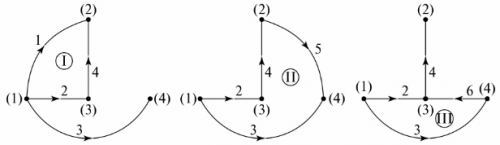
圖樹中缺失的分支數等於電路的獨立迴路數。在這個例子中，這是三個分支，三個獨立的循環。獨立循環的配置可以通過將圖樹的節點與圖樹上未指定的分支順序連接來獲得。例如，對於圖 1 中的圖樹。 5，和獨立的輪廓示於圖。 6.

米。 6.通過圖樹確定獨立輪廓

選擇一個選項來配置獨立電路以計算電路是在電路分析期間執行的。您應該選擇這樣的輪廓，以便計算盡可能簡單，即系統中相關方程的數量最少。

拓撲方程建立了電路中電壓和電流之間的關係，方程的數量和類型不取決於分支中包含哪些元素。拓撲方程包括由以下組成的方程 根據基爾霍夫定律.