電場中的電子

電子在電場中的運動是電氣工程中最重要的物理過程之一。圖 讓我們看看這是如何在真空中發生的。讓我們首先考慮一個電子在均勻電場中從陰極移動到陽極的例子。

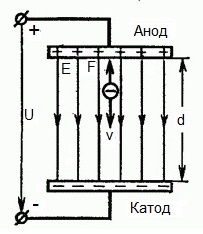
下圖顯示了一種情況 電子 以可忽略的小初始速度（趨於零）離開負電極（陰極）並進入 在均勻電場中存在於兩個電極之間。

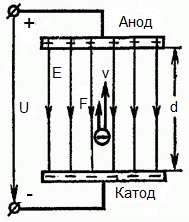
在電極上施加恆定電壓U，電場具有相應的強度E。電極之間的距離等於d。在這種情況下，一個力 F 將從場的一側作用在電子上，它與電子的電荷和場的強度成正比：

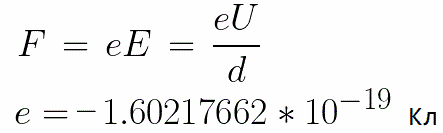
由於電子帶負電荷，該力將針對場強矢量 E。因此，電子將被電場沿該方向加速。

電子所受的加速度與作用在其上的力 F 的大小成正比，與電子的質量 m 成反比。由於場是均勻的，給定圖片的加速度可以表示為：

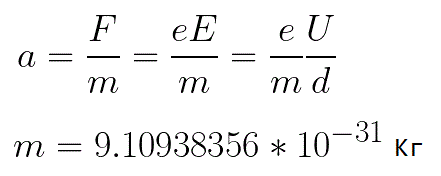
在這個公式中，電子的電荷與其質量的比率是電子的比電荷，一個物理常數的量：

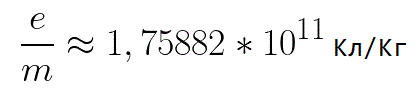
所以電子處於加速電場中，因為初速度 v0 的方向與場側力 F 的方向重合，因此電子作勻速運動。如果沒有障礙物，它將沿著電極之間的路徑 d 以一定的速度 v 到達陽極（正極）。在電子到達陽極的那一刻，其動能將相應地等於：

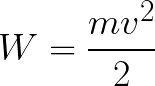
由於電子沿著整個路徑 d 被電場力加速，因此它獲得了這種動能，這是作用在電場一側的力所做的功的結果。這項工作等於：

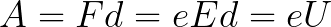
則電子在場中運動所獲得的動能可由下式求得：

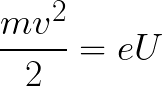
也就是說，在電位差為U的點之間加速電子無非是場力的功。

在這種情況下，為了表示電子的能量，使用“電子伏特”這樣的測量單位會很方便，它等於電子在 1 伏特電壓下的能量。並且由於電子電荷是恆定的，那麼 1 伏特也是一個恆定值：

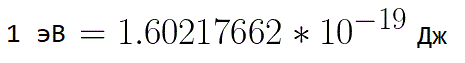
根據前面的公式，您可以輕鬆確定電子在加速電場中移動時其路徑上任意一點的速度，只需知道它在加速時通過的電勢差：

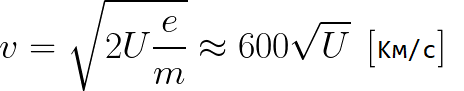
正如我們所見，電子在加速場中的速度僅取決於其路徑的終點和起點之間的電勢差 U。

想像一下，電子開始以可以忽略不計的速度遠離陰極，陰極和陽極之間的電壓為 400 伏。在這種情況下，在到達陽極的那一刻，它的速度將等於：

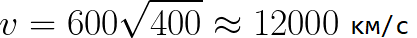
也很容易確定電子行進電極之間的距離 d 所需的時間。由靜止勻加速運動，求平均速度為最終速度的一半，則在電場中加速飛行的時間為：

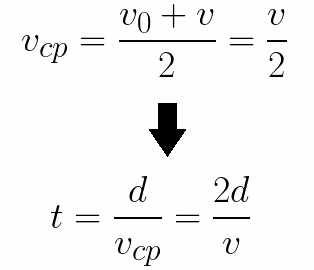
現在讓我們考慮一個電子在減速均勻電場中移動的例子。也就是說，電場的方向和以前一樣，但電子開始向相反的方向移動——從陽極到陰極。

假設電子以某個初始速度 v 離開陽極，並開始朝陰極方向移動。在這種情況下，從電場一側作用在電子上的力 F 將針對從陰極到陽極的電場強度矢量 E。

它會開始降低電子的初始速度，也就是說，場會使電子減速。這意味著在這些條件下的電子將開始均勻且均勻地緩慢移動。情況描述如下：“電子在減速電場中運動”。

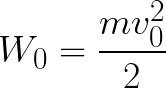
從陽極開始，電子開始以非零動能運動，在減速過程中動能開始減少，因為能量現在被消耗在克服場作用在電子上的力上。

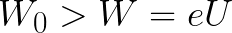
如果電子離開陽極時的初始動能立即大於場必須消耗的能量以加速電子從陰極移動到陽極（如第一個示例），則電子將行進一段距離 d，儘管有剎車，但最終會到達陰極。

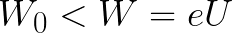
如果電子的初始動能小於這個臨界值，那麼電子就不會到達陰極。在某一點它會停止，然後開始均勻加速運動回到陽極。結果，場會將停止過程中消耗的能量返回給它。

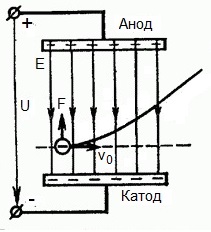
但是，如果一個電子以速度 v0 在電場作用區內以直角飛行呢？顯然，該區域場側的力是針對電子從陰極到陽極的，即與電場強度矢量E相反。

這意味著現在電子有兩個運動分量：第一個 - 速度為 v0 垂直於場，第二個 - 在場側指向陽極的力的作用下均勻加速。

事實證明，電子飛入作用域後，沿著拋物線軌跡運動。但飛出場作用區後，電子將繼續沿直線軌跡作慣性勻速運動。